Hydraulic diameter

Turbulent Flow

The hydraulic diamater d_H is calculated by the assumption that pressure drop and average speed are equal in the completely filled tube with d_H and the noncircular cross section. The volume flow has to be converted:

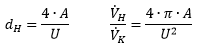A : noncircular cross section
U : noncircular circumference

rectangular channel:

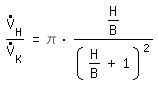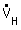: volume flow in tube with d_H

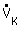: volume flow in rectangular channel
H : channel height
B : channel width

H / B	0,2	0,4	0,6	0,8	1
/	0,44	0,64	0,74	0,78	0,79

Laminar Flow

The hydraulic diameter d_H can be determined for several cross sections such that pressure drop and volume flow are equal in the completely filled round tube with d_H and the noncircular cross section.

rectangular channel:

d_H = H · f (H/B)

H: channel height
B: channel width, B > H
f(H/B): derivation see below

H/B	0,2	0,4	0,6	0,8	1
f (H/B)	1,96	1,59	1,37	1,22	1,09

Theory

Turbulent Flow

At turbulent flow you choose a hydraulic diameter that leads to equal average wall shear stress and pressure drop in the completely filled round tube with d_H and the noncircular cross section. The equilibrium of forces for the round tube and the noncircular cross section describe the following equations:

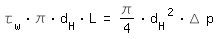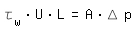		L: length

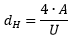The same average speed leads to the same pressure drop in both systems. The ratio of average wall shear stress to average speed is approximately equal in both systems, since the velocity profile is rather flat in turbulent flow.

The volume flow has to be converted. With the same average speed we derive:

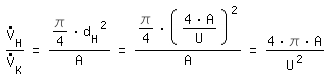
rectangular channel:

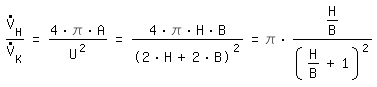
Laminar Flow

For laminar flow good approximation equations exist for numerous noncircular cross sections that describe the volume flow as a function of pressure drop. [Berker 1963] lists closed form solutions for the speed profile of several noncirular cross sections.

For a rectangular channel with BxH (B>H) we can write:

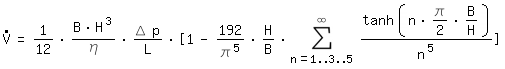
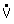: volume flow η: dynamic viscosity L: channel length

For B>>H this equation converges towards the solution for two parallel plates, also called Couette Flow (see appendix for more details):

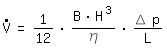
The hydraulic diameter is derived as follows:

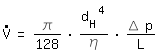		laminar pipe flow (Hagen Poiseuille Flow) (see appendix for more details)
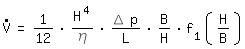		laminar flow in rectangular channel

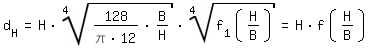
Hagen Poiseuille and Couette Flow

Literature

[Berker 1963] Tapis Berker, Encyclopedia Of Physics / Handbuch der Physik, Edited by S. Flügge, Springer-Verlag 1963, page 70