Pressure loss of the viscous flow through straight pipes
| Δ p = f · l/d · ρ/2 · v2 (Darcy-Weisbach formula) |
| dimensioned variables (metric as example) | ||
| Δ p | [kg/(m s²) = 10-5 bar = 10-2mbar] | : Pressure loss of the straight pipe |
| l | [m] | : Length |
| d | [m] | : Internal Diameter |
| ρ | [kg/m³] | : Density |
| v | [m/s] | : Average speed in the pipe |
| η | [kg/(m s) = Pas] | : Dyn. Viscosity |
| ε | [m] | : Roughness |
| dimensionless values | ||
| Re | [-] | : Reynolds number Re = ρ v d / η |
| f | [-] | : Darcy Friction Factor |
For Re < 2320 (laminar flow) the Darcy Friction Factor is calculated according to Hagen-Poiseuille:
f = 64 / Re
 Hagen Poiseuille and Couette Flow
Hagen Poiseuille and Couette Flow
For Re > 2320 (turbulent flow) the Darcy Friction Factor is calculated according to [Colebrook 1939, page 137]:
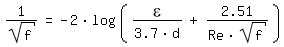
|
For Re => ∞ (completely turbulent flow) the equation of Colebrook converges to the equation of [Prandtl 1933, page 110] according to Kármán:
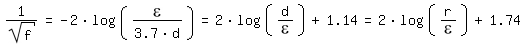
and for ε/d => 0 (smooth pipe) to the equation of [Prandtl 1933, page 111]:
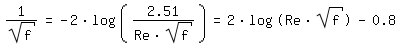
Laminar flow is possible for Re < 8000 [VDI 1984, page Lb1]. In the critical transition
zone (2320 <= Re < 8000) the value of the Darcy Friction Factor might be overestimated
by the means of calculation presented above.
The Moody-diagram [Moody 1944, page 672] is a successful illustration of the equations
presented above.
 |
 | |
| Moody Re: 10-106 | Moody Re: 100-108 | |
With 1/f^0,5 = Re/200 · ε /d and 1/f^0,5 = 2log(r/ε) + 1,74 [Moody 1944, page 676] draws a line between the transition zone and the completely turbulent pipe flow.
| Literature |
| [Colebrook 1939] C.F. Colebrook, Turbulent Flow in Pipes, with particular reference to the Transition Region between the Smooth and Rough Pipe Laws, Journal of The Institution of Civil Engineers, Volume 11, 1939 |
| [Moody 1944] L.F.Moody, Friction Factors of Pipe Flow, Transactions of the ASME, Volume 66, 1944 |
| [Prandtl 1933] L. Prandtl, Neuere Ergebnisse der Turbulenzforschung, Zeitschrift des Vereins Deutscher Ingenieure, Band 77, 1933 |
| [VDI 1984] VDI-Wärmeatlas 4. Auflage 1984 |